সাইন, কোসাইন এবং ট্যানজেন্ট দৈনন্দিন স্কুল জীবনে ব্যাপকভাবে ব্যবহৃত হয় এবং সেগুলি সম্পর্কে সচেতন হওয়া অপরিহার্য
-1jy7orqt0u4hi.png "আর্থ সম্পাদকীয়"){kind=small}
বোঝার জন্য ত্রিকোণমিতিত্রিভুজগুলির গাণিতিক অধ্যয়ন, একটি বড় চ্যালেঞ্জ হতে পারে, এমনকি প্রাপ্তবয়স্কদের জন্য যাদের এলাকায় প্রচুর জ্ঞান রয়েছে। হিসেব ও সূত্রগুলো ‘বর্ণমালার স্যুপ’-এর মতো মনে হলেও কিছুটা চেষ্টা করলে বিষয়টা বোঝা ও এগিয়ে যাওয়া সম্ভব।
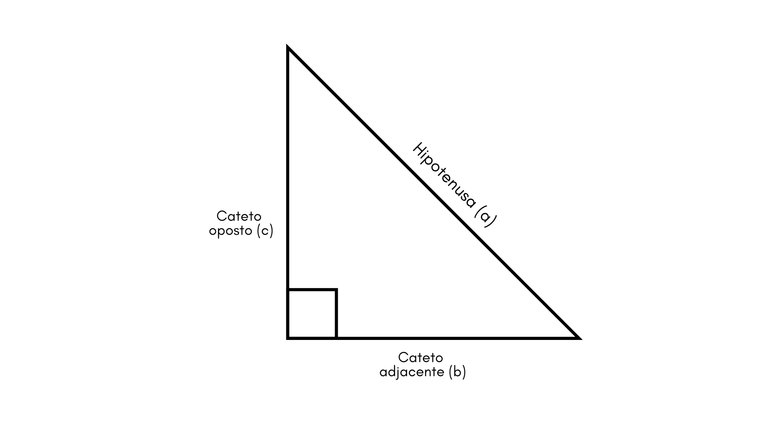
বিষয়টি বোঝার জন্য, আপনাকে বুনিয়াদি এবং এই পুরো সিস্টেমটি কীভাবে কাজ করে তা বুঝতে হবে। ত্রিকোণমিতি হল একটি অধ্যয়ন যেখানে ত্রিভুজের কোণ এবং বাহু গণনা করা হয়। দ সমকোণী ত্রিভুজ সমান কোণ সহ তিনটি বাহু দ্বারা গঠিত হয় 90º. এতে, প্রতিটি পক্ষের একটি নাম রয়েছে:
- হাইপোটেনাস (ক): দীর্ঘতম দিক এবং ডান কোণের একটি “সামনে”।
- বিপরীত ক্যাথেটাস (c): ঠিক যেমন নামটি সুপারিশ করে, এটি দীর্ঘতম দিকের বিপরীতে।
- সংলগ্ন ক্যাথেটাস (b): একটি নির্দিষ্ট কোণের পাশে এবং তীব্র গঠন করে।
একসাথে, তারা পিথাগোরিয়ান উপপাদ্য গঠন করে: a2 = b2 + c2। যেকোনো ত্রিভুজের কোণের সমষ্টি 180°।
যদিও বেশিরভাগ লোকের প্রাথমিক শিক্ষার সময় ত্রিকোণমিতির সাথে যোগাযোগ থাকে, স্কুলে, এই গণনাটি পেশাদার এবং প্রতিষ্ঠান দ্বারা ব্যাপকভাবে ব্যবহৃত হয়। উদাহরণস্বরূপ, মার্কিন যুক্তরাষ্ট্রের ন্যাশনাল অ্যারোনটিক্স অ্যান্ড স্পেস অ্যাডমিনিস্ট্রেশন এজেন্সি নাসা পোর্টালে ব্যাখ্যা করা হয়েছে যে গবেষণাটি বিমান এবং চালনার উন্নয়নে ব্যবহৃত হয়। এখন, আমরা পরবর্তী ধাপে যেতে পারি।
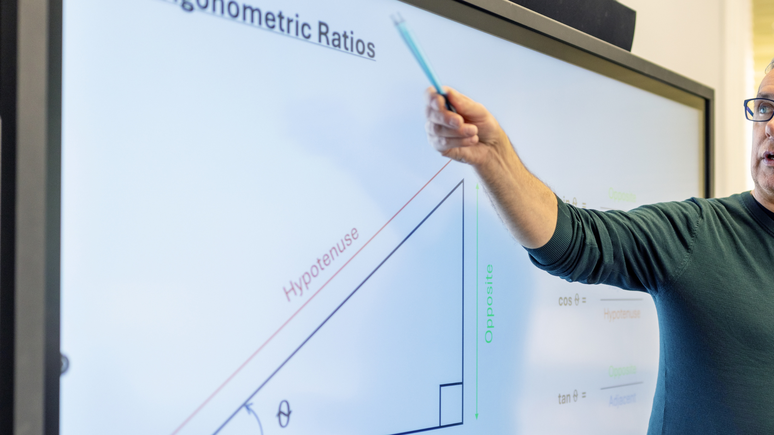
সাইন, কোসাইন এবং স্পর্শক: তারা কি এবং তারা কি জন্য?
সাইন, কোসাইন এবং ট্যানজেন্ট হল ত্রিকোণমিতির তিনটি অনুপাত। এগুলি একটি সমকোণী ত্রিভুজের বাহুগুলি গণনা করতে ব্যবহৃত হয় এবং গণনাগুলি তৈরি হওয়ার সাথে সাথে সূত্রগুলি তৈরি হয়।
সূত্র
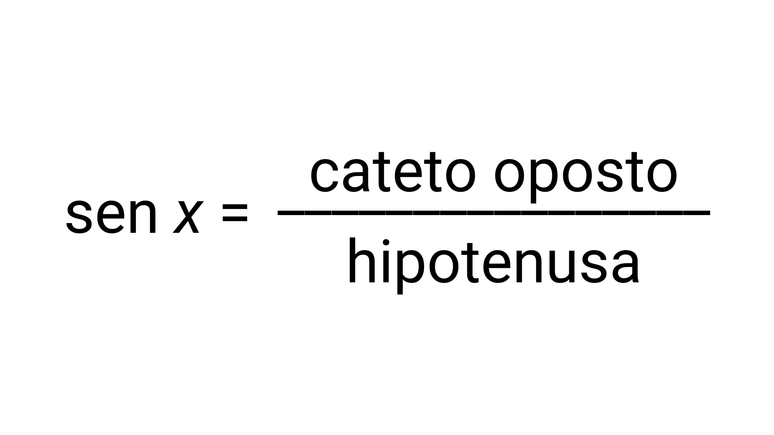
সমকোণী ত্রিভুজের বিপরীত বাহু এবং কর্ণের মধ্যে চিহ্নিত প্রথম অনুপাতকে বলা হয় স্তন. এর সমতুল্য সূত্র হল: sin x = c/a.
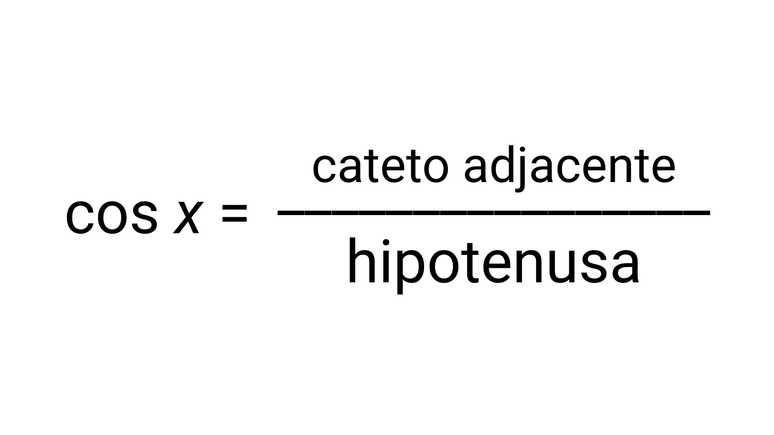
দ্বিতীয় কারণ, সংলগ্ন দিক এবং কর্ণের মধ্যে চিহ্নিত করা হয়, বলা হয় কোসাইন. সূত্রটি সমতুল্য: cos x = b/a.
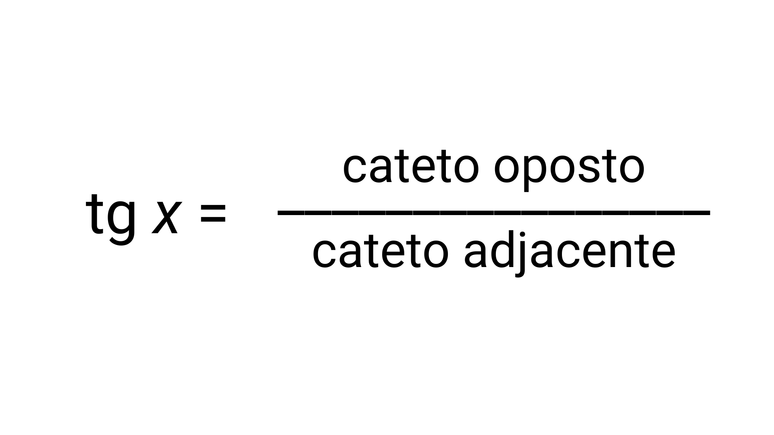
তৃতীয় কারণ, বিপরীত এবং সন্নিহিত পক্ষের মধ্যে চিহ্নিত, বলা হয় স্পর্শক. সূত্রটি সমতুল্য: tg x = c/b.
