আমি একটি হয়েছে ব্যবধানে পুনরাবৃত্তি (SR) দেরী হিসাবে লাথি. মোচিআমি যে SR সফ্টওয়্যারটি ব্যবহার করি, সেটির একটি পরিবর্তিত সংস্করণ ব্যবহার করে সুপারমেমো এসএম-2 কার্ড শিডিউল করার জন্য অ্যালগরিদম। পার্থক্যগুলি হল:
- কার্ডের ইজ ফ্যাক্টর (EF) পারফরম্যান্সের প্রতিক্রিয়াতে সামঞ্জস্য করা হয় না, তবে ম্যানুয়ালি পরিবর্তন করা যেতে পারে। ন্যায্যতা হল এটি SM-2 নামক একটি কথিত সমস্যা এড়িয়ে যায় “জাহান্নাম সহজ”.
- আপনি একটি কার্ড ব্যর্থ হলে, পরবর্তী পর্যালোচনা ব্যবধান কিন্তু রিসেট করা হয় না খারাপ বেশী.
ব্যবধান অর্ধেক করা আমি অপছন্দ করি, কারণ মাঝে মাঝে আমি প্রথম কয়েক মাস একটি কার্ড মনে রাখি, তারপরে এটি ভুলে যাই এবং এই অদ্ভুত লিম্বো অবস্থায় প্রবেশ করি যেখানে রিভিউগুলি আমার পক্ষে কার্ডটি পুনরায় শেখার জন্য যথেষ্ট নয়, তাই আমি পর্যায়ক্রমে শুরু করি এটা প্রত্যাহার এবং এটি ব্যর্থ.
কিন্তু আমি সহজ ফ্যাক্টরের পরিবর্তনের প্রভাব বুঝতে পারিনি। তাই আমি অ্যালগরিদম দেখার সিদ্ধান্ত নিয়েছি। এবং, যেহেতু আমি কী তৈরি করি না, আমি বুঝতে পারি না, আমি মরিচায় এটির একটি সহজ বাস্তবায়ন লিখেছি।
আরও কিছু ছাড়াই, কোড হল এখানে. নিম্নলিখিত কি একটি ব্যাখ্যা.
কেন আমরা একটি অ্যালগরিদম প্রয়োজন? আমরা প্রতিদিন প্রতিটি কার্ড ড্রিল করতে পারি, কিন্তু এটি একটি জীবন্ত দুঃস্বপ্ন হবে এবং আপনার কাছে ~200 ফ্ল্যাশকার্ডের বেশি থাকতে পারে না। সময়সূচী মানুষের স্মৃতির একটি সহজ, পরিমাণগত মডেল হিসাবে কাজ করে। মডেলটি যত ভাল হবে, তত বেশি আমরা দীর্ঘমেয়াদী স্মৃতিতে প্রতিশ্রুতিবদ্ধ হতে পারি এবং আমাদের অধ্যয়নের জন্য কম সময় ব্যয় করতে হবে।
আ আইটেম জ্ঞানের একটি পারমাণবিক অংশ, একটি ফ্ল্যাশকার্ড হিসাবে উপস্থাপিত: একটি প্রশ্ন-উত্তর জোড়া যা সেই জ্ঞানের অস্তিত্ব পরীক্ষা করে। একটি আইটেমের অবস্থা দ্বারা প্রতিনিধিত্ব করা হয়:
- দ সহজীকরণ ফ্যাক্টর $EF$, যা দ্বৈত অসুবিধা। এটি $(1.3, +\infty)$ রেঞ্জের একটি বাস্তব সংখ্যা। প্রাথমিক মান হল $2.5$।
- এর সংখ্যা পুনরাবৃত্তি $n$, যা কার্ডটি পরপর কতবার সঠিকভাবে ফেরত নেওয়া হয়েছে।
একটি কার্ডের অবস্থা থেকে, আমরা তার গণনা করতে পারি ব্যবধান: সাম্প্রতিকতম পরীক্ষার পর কত দিন আইটেমটি আবার পর্যালোচনা করা উচিত। ব্যবধান গণনা পুনরাবৃত্তির সংখ্যার উপর একটি পুনরাবৃত্তি সম্পর্ক দ্বারা সংজ্ঞায়িত করা হয়:
\(\beginalign* I(0) &= 0 \\ I(1) &= 1 \\ I(2) &= 6 \\ I(n) &= I(n-1) \times \textEF \endalign *\)
বদ্ধ ফর্ম অভিব্যক্তি হল:
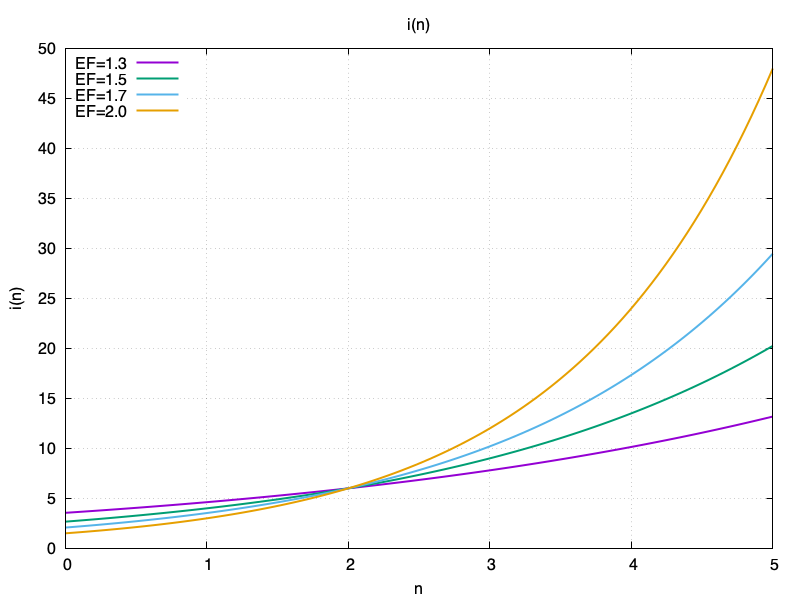
\(I(n) = 6 \times \textEF^(n-2)\)
সঠিক পুনরাবৃত্তি এবং EF এর একটি ফাংশন হিসাবে:
একটি আইটেম পরীক্ষা করার জন্য, ব্যবহারকারীকে প্রশ্ন দেখানো হয়, তারপর তারা মানসিকভাবে উত্তরটি স্মরণ করে এবং প্রকৃত উত্তরটি প্রকাশ করে। তারপর ব্যবহারকারী নির্বাচন করে তাদের কর্মক্ষমতা রেট গুণমান এই তালিকা থেকে তাদের প্রতিক্রিয়া:
- 0 = ব্ল্যাকআউট। কোন প্রত্যাহার.
- 1 = ভুল প্রতিক্রিয়া; কিন্তু উত্তর, একবার প্রকাশিত, মনে ছিল.
- 2 = ভুল প্রতিক্রিয়া; কিন্তু উত্তর মনে করা সহজ বলে মনে হচ্ছে.
- 3 = কষ্ট করে স্মরণ করা।
- 4 = দ্বিধা সহকারে স্মরণ করা হয়েছে।
- 5 = নিখুঁতভাবে স্মরণ করা হয়েছে।
$(0,2)$ এ গুণমানের মানগুলি উপস্থাপন করে ভুলে যাওয়া.
যখন একটি আইটেম পরীক্ষা করা হয়, এবং আমাদের একটি গুণমান থাকে, তখন আইটেমের অবস্থা আপডেট করতে হবে।
ব্যবহারকারী উত্তর ভুলে গেলে, পুনরাবৃত্তি গণনা শূন্য সেট করা হয়। এর মানে ব্যবধানটিও রিসেট করা হয়েছে: আপনাকে স্ক্র্যাচ থেকে কার্ডটি পুনরায় শিখতে হবে।
\(n'(n, q) = \begincases 0 & q \in(0,2) \\n+1 & \textotherwise\endcases\)
প্রতিক্রিয়া মানের সাথে সমানুপাতিক একটি মাত্রা যোগ করে EF আপডেট করা হয়:
\(\textEF'(\textEF, q) = min(1.3, \textEF + f(q))\)
কোথায়:
\(f(q) = -0.8 + 0.28q – 0.02*q^2\)
গুণগতভাবে, $f(q)$ এর মত দেখাচ্ছে:
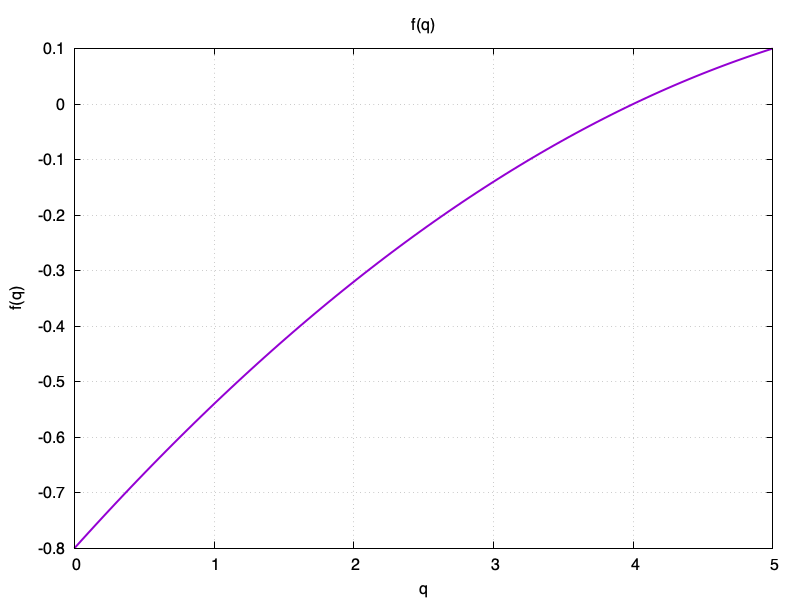
তাই নিখুঁত প্রত্যাহার থেকে কম কিছুর জন্য EF হ্রাস পায় (এবং পরবর্তী ব্যবধানটি ছোট), এবং শুধুমাত্র নিখুঁত প্রত্যাহার একটি কার্ডকে কম কঠিন করে তোলে। $q=4$ এ কিছুই পরিবর্তন হয় না।
এবং তাই আমরা আরাম জাহান্নাম পেতে পারি: ইএফকে নীচে ঠেলে দেওয়া, বা এটিকে একই রাখা, এটিকে উপরে ঠেলে দেওয়ার চেয়ে অনেক সহজ।
অ্যালগরিদমের চূড়ান্ত অংশটি হল, একটি পর্যালোচনা সেশনের শেষে, $(0, 3)$-এ গুণমান সহ সমস্ত আইটেম আবার পরীক্ষা করা উচিত যতক্ষণ না তাদের সকলেরই $(4,5)$-এ প্রত্যাহার গুণমান থাকে৷
স্কেলার প্রকার:
pub type Repetitions = u32;
pub type Ease = f32;
pub type Interval = u32;
সাধারনত আমি স্মার্ট কনস্ট্রাক্টর সহ নতুন টাইপ ব্যবহার করব রেঞ্জ সহ প্রকারগুলি উপস্থাপন করতে (যেমন EF এর সর্বনিম্ন মান 1.3)। কিন্তু এটি কোডটিকে আরও কুৎসিত করে তুলবে, তাই পরিবর্তে আমি লিখেছি:
pub const INITIAL_EF: Ease = 2.5;
const MIN_EF: Ease = 1.3;
fn min(ef: Ease) -> Ease
if ef < MIN_EF
MIN_EF
else
ef
গুণমান স্বাভাবিকভাবেই একটি enum হিসাবে প্রতিনিধিত্ব করা হয়:
#(derive(Debug, Copy, Clone, PartialEq))
pub enum Quality
/// Complete blackout.
Blackout = 0,
/// Incorrect response; the correct one remembered.
Incorrect = 1,
/// Incorrect response; where the correct one seemed easy to recall.
IncorrectEasy = 2,
/// Correct response recalled with serious difficulty.
Hard = 3,
/// Correct response after a hesitation.
Good = 4,
/// Perfect response.
Perfect = 5,
দুটি পূর্বাভাস দিয়ে, এই গুণমানের মানটি ভুলে যাওয়া বোঝায় কিনা এবং সেশনের শেষে আইটেমটি পুনরাবৃত্তি করা দরকার কিনা তা পরীক্ষা করতে:
impl Quality
pub fn forgot(self) -> bool
match self Self::Incorrect
pub fn repeat(self) -> bool
match self
Self::Blackout
একটি আইটেমের অবস্থা হল তার $n$ এবং $\textEF$ এর মান (সঠিক নির্ধারিত তারিখের টাইমস্ট্যাম্প সিস্টেমের বাইরে প্রয়োগ করা হবে):
pub struct Item
n: Repetitions,
ef: Ease,
একটি আইটেম দেওয়া, আমরা এর ব্যবধান গণনা করতে পারি:
impl Item
pub fn interval(&self) -> Interval
let r = self.n;
let ef = self.ef;
match self.n
0 => 0,
1 => 1,
2 => 6,
_ =>
let r = r as f32;
let i = 6.0 * ef.powf(r - 2.0);
let i = i.ceil();
i as u32
দ Item::review পদ্ধতি একটি আইটেম গ্রাস করে এবং একটি মানের রেটিং দেওয়া, তার অবস্থা আপডেট করে:
impl Item
pub fn review(self, q: Quality) -> Self
Self
n: np(self.n, q),
ef: efp(self.ef, q),
কোথায়:
fn np(n: Repetitions, q: Quality) -> Repetitions
if q.forgot()
0
else
n + 1
fn efp(ef: Ease, q: Quality) -> Ease
let ef = min(ef);
let q = (q as u8) as f32;
let ef = ef - 0.8 + 0.28 * q - 0.02 * q * q;
min(ef)



